2 Neural Networks
Outline
In this chapter, we look at the functioning of neurons and neural networks from an information-processing perspective. This perspective is often missing in textbook introductions to neurophysiology, but can be extremely helpful for illustrating how exactly cellular processes within and between neurons enable computations and cognition. In other words, neural networks can bridge physiology and psychology.
For a brief introduction to neural networks and their everyday applications, watch the following video:
Information Processing & the Integrate-and-Fire Model
Vision scientist David Marr first proposed that neural systems can profitably be examined from three levels of analysis: the implementational level, the algorithmic level, and the computational level. The implementational level of analysis is concerned with the physical substrate of a system. In a computer, that would mean examining the hardware of the computer: the transistors and other electrical components. In a brain, that would mean examining the “wetware” of the brain: the neurophysiological details of how neurons work. At the highest level of analysis, the computational level is concerned with the function of a system. How can we succinctly describe what a particular computer circuit or neural network does? According to computational neuroscientists Randall O’Reilly and colleagues, neurons can be thought of functionally as detectors. Like smoke detectors, neurons are tuned to detect certain properties. If that property is present, a neuron will fire, otherwise it will not.[1] On one very simple level of description, the visual system can be thought of as a hierarchy of detectors, beginning with the detection of simple “pixels” and lines and ending in the recognition of objects like faces and chairs.
The algorithmic level of analysis bridges the implementational and computational levels. It is concerned with how the functioning of a system can be realized by its physical substrate. This requires abstracting from the physical substrate (hardware or wetware) in such a way as to see how, for example, ion movement in neurons could yield the detection of a line in the visual field. The resulting abstraction is a set of rules, called an algorithm, which could in principle be realized by many different physical substrates. You may have already seen an example of an algorithm in the last chapter, which described the rules governing how a cellular automaton works.
In order for any system, including neural networks, to process information, it must have two properties:
- The system must have units/cells that can alternate between two states.
- The state of one unit/cell must be a function of the influence of other units/cells.
Neurons can be thought of as having a default state when they are not processing information. In this default state, neurons are not systematically generating action potentials.[2] When they are not generating an action potential, the electrical charge of the neuron is at its resting membrane potential, in which the inside of the neuron is negative relative to the outside. We may represent this default state as a 0, like a bit of information (see figure below).
In order to process information, a neuron must be able to switch to an active state, and then return to its default state. A neuron changes to its active state—that is, it generates an action potential, causing the polarity of the membrane potential to become positive—when the accumulation of excitatory post-synaptic potentials raises a neuron’s membrane potential above its threshold for firing. We can represent this active state as a 1, as in the figure below. Following an action potential, the segment of the neuron which generated it returns to its resting potential (0). From this perspective, we can think of individual neurons as flipping between a 0 and a 1, and networks of neurons as having neurons in different combinations of 0s and 1s, just as we might think of information processing in a computer as being grounded in 0s and 1s.
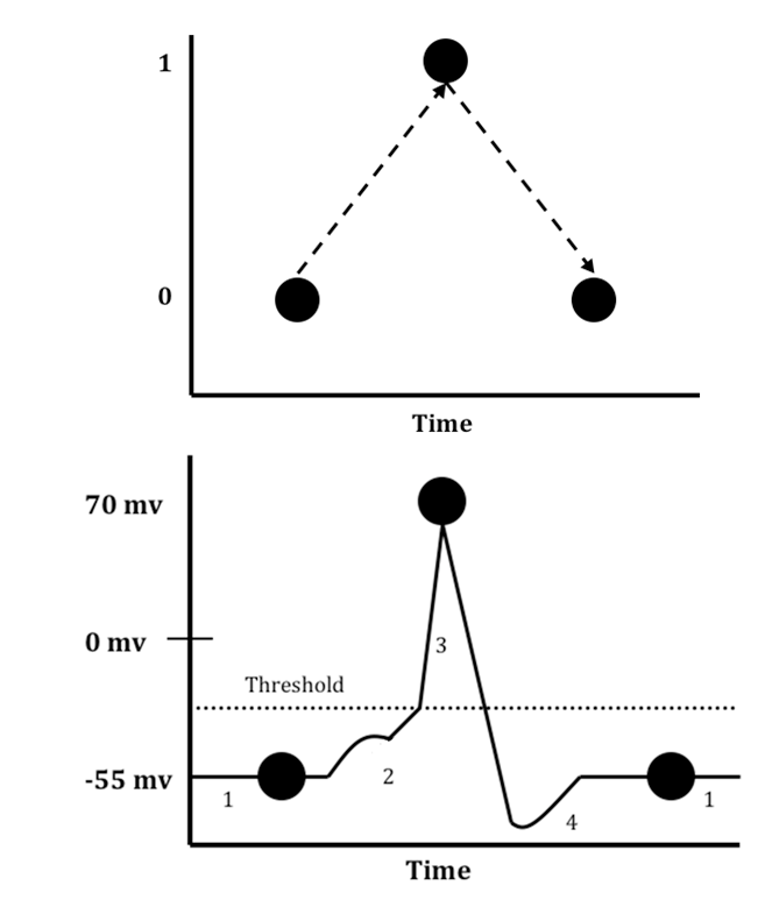
One classic algorithm for representing how neurons are influenced by other neurons is called the “integrate-and-fire” model. According to this model, a neuron integrates all of the inputs it is receiving from other neurons, and if the total input exceeds some threshold, the neuron will fire. At a functional (computational) level, this is like a smoke detector which will sound when it detects a certain level of smoke in the environment. For a simple integrate-and-fire neuron, there are three easy steps to determine whether a neuron will fire (1) or not (0) as a function of its inputs:
- Step 1: Multiple the activity of an input neuron with the connection strength between that neuron and its target neuron. Do this for all of the inputs to a particular target neuron.
- Step 2: Add together all of the results from Step 1.
- Step 3: If the result of Step 2 meets or exceeds some predefined threshold, the neuron will fire. Otherwise, it will not.
For simplicity in the examples that follow, connection strengths between neurons will range from -1 to 1, like a correlation. If the connection strength is -1, the input neuron will have a strong inhibitory influence on the target neuron. In other words, the target neuron will be taken further from the threshold it needs to reach in order to fire. If the connection strength is -0.5, the input neuron will have a moderate inhibitory influence on the target neuron. A connection strength of 0 means that the input neuron has no influence on the target neuron. And connection strengths of 0.5 and 1 will result in moderate and strong excitatory influences, respectively, on the target neuron. That is, the neuron will be brought closer to the threshold needed to fire.
Think Critically 2.1
What neurobiological mechanisms might correspond to the “connection strength” between neurons? To answer this question, think about the processes happening in the pre-synaptic axon terminal, the synaptic cleft, and the post-synaptic dendrite.
We see from the above how neural networks embody the two properties of an information processing system. It has cells that can alternate between two states (0 = default state = resting membrane potential; 1 = active state = action potential). And which state a neuron is in is a function of the input coming from pre-synaptic neurons. If a neuron is unable to switch from one state to the other, and so unable to flexibly impact downstream neurons, then it is no longer able to process information. Indeed, many neurotoxins, such as the tetrodoxotin found in blowfish, increase how long a neuron is in either its default or active state. This can ultimately cause paralysis or death. Many different types of neurotoxin are generated by the a wide range of creatures in nature, precisely with the goal to disrupt information processing in their potential predator or prey organisms.
| Level of Analysis | Application to Neurons |
| Computational (functional) | Detector |
| Algorithmic | Integrate-and-Fire Model |
| Implementational | Neurophysiology |
This table shows examples of how the operation of neurons can be viewed from three different levels of analysis.
Emergence of Logical Functions
Just as with the examples of emergence in the last chapter, the power of neurons rests in their interactions. Let’s look at several examples of small networks composed of integrate-and-fire neurons.[3]
Consider a neural network consisting of just three neurons—two that serve as inputs projecting to one output neuron (see figure below). Imagine that the threshold of the output neuron is 0.5, and the connection strengths between each input-output pair are also 0.5. What we are interested in is how the output neuron responds to different combinations of the input neurons.
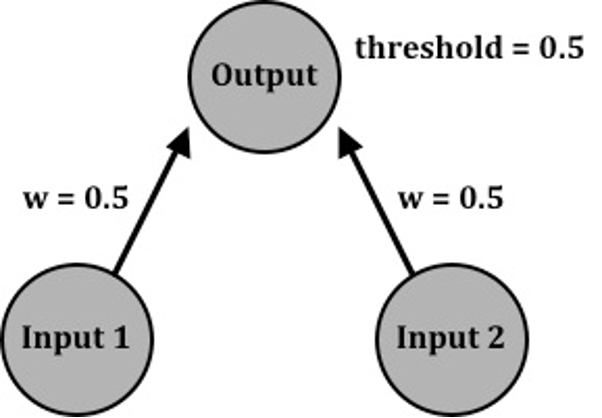
Neural network which computes the “inclusive-or” logical function. Weights (w) refer to the synaptic strength connecting either the first or second input unit to the sole output unit.
To better visualize this, let’s construct a truth table (see table below), which lists the four possible combinations of input values (0 = not firing; 1 = firing). The Output is determined by applying the three integrate-and-fire steps.
|
Input 1 |
Input 2 |
Output |
|
0 |
0 |
? |
|
1 |
0 |
? |
|
0 |
1 |
? |
|
1 |
1 |
? |
Truth table for showing the relationships between input and output neuron activity levels.
Let’s work through each combination of input values:
Combination: Input 1 = 0, Input 2 = 0
- Step 1:
- Input into Output neuron coming from Input 1 neuron: 0 * 0.5 = 0
- Input into Output neuron coming from Input 2 neuron: 0 * 0.5 = 0
- Step 2: 0 + 0 = 0
- Step 3: Because 0 is less than the threshold of 0.5, the Output will not fire. Therefore, the Output for this combination is 0.
Combination: Input 1 = 1, Input 2 = 0
- Step 1:
- Input into Output neuron coming from Input 1 neuron: 1 * 0.5 = 0.5
- Input into Output neuron coming from Input 2 neuron: 0 * 0.5 = 0
- Step 2: 0.5 + 0 = 0.5
- Step 3: Because 0.5 equals the threshold of 0.5, the Output will fire. Therefore, the Output for this combination is 1.
Combination: Input 1 = 0, Input 2 = 1
- Step 1:
- Input into Output neuron coming from Input 1 neuron: 0 * 0.5 = 0
- Input into Output neuron coming from Input 2 neuron: 1 * 0.5 = 0.5
- Step 2: 0 + 0.5 = 0.5
- Step 3: Because 0.5 equals the threshold of 0.5, the Output will fire. Therefore, the Output for this combination is 1.
Combination: Input 1 = 1, Input 2 = 1
- Step 1:
- Input into Output neuron coming from Input 1 neuron: 1 * 0.5 = 0.5
- Input into Output neuron coming from Input 2 neuron: 1 * 0.5 = 0.5
- Step 2: 0.5 + 0.5 = 0.5
- Step 3: Because 1 is greater than the threshold of 0.5, the Output will fire. Therefore, the Output for this combination is 1.
Now, we can enter all of these Output values into our Truth Table:
|
Input 1 |
Input 2 |
Output |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
Truth table for “inclusive-or” logical function.
This network implements a particular logical function called “inclusive-or”. This means that the output will fire if either one or the other input fires (is 1), or both inputs fire. This is different from what we normally think of by “or”, which is that one thing or another will happen, but not both. That is called “exclusive-or”, and we will examine that case later.
Let’s reflect on the present network. We have three neurons—two of which we just decide whether they are on or off, in all possible combinations, and the third one behaves like a smoke detector. And yet, the network as a whole has implemented a logical function. That is emergence. And the interactions between the neurons were the key to producing it.
There is nothing magical about the value 0.5 for each of the weights, or the value 0.5 for the threshold. We could have chosen different numbers and achieved an identical result. Verify this by doing Activity 2.1.
Activity 2.1: Interactions in a Simple Neural Network 1
Suppose that the connection strength from Input 1 to the Output is 0.3, from Input 2 to the Output is 0.8, and the threshold is 0.3. Verify that this new set of weights and threshold will yield the inclusive-or function by working through the three integrate-and-fire steps and entering the results in a truth table:

There are combinations of numbers, however, which will not produce inclusive-or. Consider the following network. This is identical to the first network, except the threshold has now been raised to 1.0. To determine which function this network implements, do Activity 2.2.
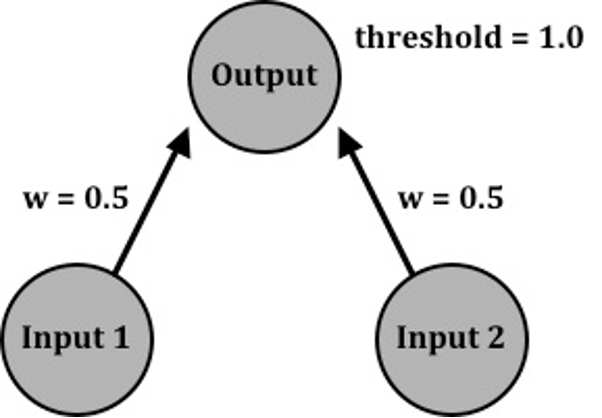
Activity 2.2: Interactions in a Simple Neural Network 2
Complete the following truth table using the set of connection weights and threshold in the figure above.

The truth table that you derived in Activity 2.2 represents the logical function “and”. The Output only fires when both Input 1 AND Input 2 are firing. We can readily see why this network has a different behavior—because the threshold of the Output neuron is higher, it takes more for it to fire. A single input is no longer enough; both are required.
From these examples, we can see that the important factor in determining which logical function is emerging is the relationship between the connection strengths and the threshold, not their actual values, per se. Note also that the meaning of the whole network has changed (from “inclusive-or” to “and”) just because it took more to get the Output smoke detector to fire. And of course, no single neuron has any idea that it is an integral part of something more meaningful, like calculating a logical function. To cement these ideas, do Activity 2.3.
Activity 2.3: Interactions in a Simple Neural Network 3
Choose another set of weights and threshold that will also produce an “and” network.
Let’s see a constructive application of the “and” logical function. Imagine that a block letter “E”, like that pictured below, is the only object in your environment, and you would like to be able to see it. Your retina’s photoreceptors can detect “pixels” of the “E”, which then feed into multiple layers of downstream neurons in the retina, lateral geniculate nucleus of the thalamus, and early visual areas in the occipital lobe. Each photoreceptor and neuron in this network can be said to represent some aspect of the environment. For example, each photoreceptor, in this example, represents a small block in the environment. Assume that each neuron in the network fires if and only if all of the neurons/photoreceptors that are connected to that neuron are also active (in other words, the overall network is a series of connected “and” networks). We can then depict the representations of the numbered neurons as in the figure below. Of course, the actual visual system is far more complex than this (see the next chapter!), but the basic idea is illustrative. For a more detailed illustration of a hierarchical model of object representation, see here.


Left: Hierarchical array of “and” networks. Right: Representations of same-numbered neurons in the neural network.
Let’s examine one more logical function, exclusive-or, and then take a look at the bigger picture. As it turns out, exclusive-or cannot be computed with just an input layer of neurons and an output neuron. Indeed, this limitation was pointed out in 1969 by researchers Minsky and Papert, and effectively halted much neural network research until the mid-1980s. Then, it was discovered that exclusive-or could be computed if you added one more layer of neurons, called “hidden” layers (see figure below).
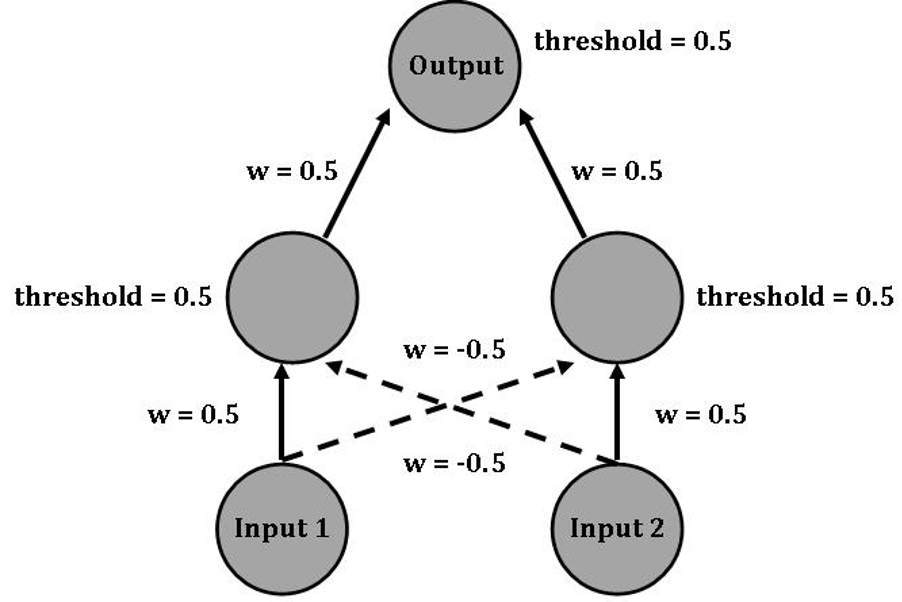
Solid lines denote excitatory (positive) connection strengths, and dashed lines denote inhibitory (negative) connection strengths.
Let’s work through this example. Note that there are more steps now because there is an additional layer. We must first see what the Hidden-layer neurons will do in response to the Input neurons, and then we can calculate how the Output neuron responds to the Hidden-layer neurons.
The case where both inputs are 0 is pretty clear—if there is nothing happening in the inputs, then there cannot be any output activity. So let’s begin with the case where Input 1 = 1 and Input 2 = 0:
Examining Hidden-layer activity for Combination: Input 1 = 1, Input 2 = 0
- Step 1:
- Input into left Hidden unit neuron coming from Input 1 neuron: 1 * 0.5 = 0.5
- Input into left Hidden unit neuron coming from Input 2 neuron: 0 * -0.5 = 0
- Input into right Hidden unit neuron coming from Input 1 neuron: 1 * -0.5 = -0.5
- Input into right Hidden unit neuron coming from Input 2 neuron: 0 * 0.5 = 0
- Step 2:
- Left Hidden unit: 0.5 + 0 = 0.5
- Right Hidden unit: -0.5 + 0 = -0.5
- Step 3:
- Left Hidden unit: Because 0.5 equals the threshold of 0.5, the left Hidden unit will fire. Therefore, its output is 1.
- Right Hidden unit: Because -0.5 is below the threshold of 0.5, the right Hidden unit will not fire. Therefore, its output is 0.
- Step 4 (Step 1 for the Output neuron):
- Input into Output neuron coming from left Hidden unit neuron: 1 * 0.5 = 0.5
- Input into Output neuron coming from left Hidden unit neuron : 0 * 0.5 = 0
- Step 5 (Step 2 for the Output neuron):
- 0.5 + 0 = 0.5
- Step 6 (Step 3 for the Output neuron):
- Because 0.5 meets the threshold of 0.5, the Output will fire. Therefore, the Output for this combination is 1.
This network is known as a symmetrical network because all of the weights projecting from the neurons on the left half of the network (Input 1 and the left-most hidden neuron) are mirrored by the same weights projecting from neurons on the right half of the network. Because this network is symmetrical, the case where Input 1 = 0 and Input 2 = 1 will have the exact same result as the case we just examined. So let’s examine the last case, where both inputs are on.
Examining Hidden-layer activity for Combination: Input 1 = 1, Input 2 = 1
- Step 1:
- Input into left Hidden unit neuron coming from Input 1 neuron: 1 * 0.5 = 0.5
- Input into left Hidden unit neuron coming from Input 2 neuron: 1 * -0.5 = -0.5
- Input into right Hidden unit neuron coming from Input 1 neuron: 1 * -0.5 = -0.5
- Input into right Hidden unit neuron coming from Input 2 neuron: 1 * 0.5 = 0.5
- Step 2:
- Left Hidden unit: 0.5 + -0.5 = 0
- Right Hidden unit: -0.5 + 0.5 = 0
- Step 3:
- Left Hidden unit: Because 0 is below the threshold of 0.5, the left Hidden unit will not fire. Therefore, its output is 0.
- Right Hidden unit: Because 0 is below the threshold of 0.5, the right Hidden unit will not fire. Therefore, its output is 0.
- Step 4 (Step 1 for the Output neuron):
- Input into Output neuron coming from left Hidden unit neuron: 0 * 0.5 = 0
- Input into Output neuron coming from left Hidden unit neuron : 0 * 0.5 = 0
- Step 5 (Step 2 for the Output neuron):
- 0 + 0 = 0
- Step 6 (Step 3 for the Output neuron):
- Because 0 is below the threshold of 0.5, the Output will not fire. Therefore, the Output for this combination is 0.
In the last case, the inhibitory connections allowed Input 1 and Input 2 to cancel each other out, which enabled the production of exclusive-or, rather than inclusive-or. The full truth-table, including the intermediary steps for calculating the Output, is shown below.

Let’s look at the bigger picture. We’ve seen how relatively simple units (neurons acting like smoke detectors) can interact to create more sophisticated products (logical functions). Interestingly, logical functions are the bedrock of how computers work. So, you can now begin to imagine how human abilities like reasoning can emerge from neurons, just as computer programs like Microsoft Word depend on electrical components. The nature of interactions in our neural networks, including the relationships between connection strengths and thresholds, as well as excitation and inhibition, determined which product emerged. Now, as it turns out, three-layer networks, like the exclusive-or network, can compute almost any function[4] and a four-layer network (created by adding one more hidden layer) can compute any computable function. Because a four-layer neural network (and therefore networks with more layers, like the brain) can compute any function, it is known as a universal computer.
Brains are universal computers. Computers are also universal computers. Clearly computers and brain are quite different and have different strengths, however. Computers excel at holding information in memory and executing quick calculations. Brains excel at recognizing patterns, which is necessary to see, hear, and touch, among many other abilities we have. In other words, while both brains and computers are universal computers, brains excel at some of those computations, while computers excel at others.
Think Critically 2.2
What are other differences between what brains and computers can do? Brainstorm a list. What is it about how brains and computers work that might give rise to those differences?
At the start of this chapter, you learned that the computational and algorithmic levels of analysis are distinct from the implementational level. The rules at the algorithmic level giving rise to logical functions at the computational level can be realized at the implementational level in either brains or computers. Logical functions could even be instantiated in entirely different types of materials—such as dominos! For a very interesting example, see this website and the video below (a domino-based demonstration of “exclusive-or” begins at 3:40).
Now, imagine other possibilities in this Think Critically box.
Think Critically 2.3
Before moving on to the next chapter, test your comprehension of the preceding material by doing Activity 2.4.
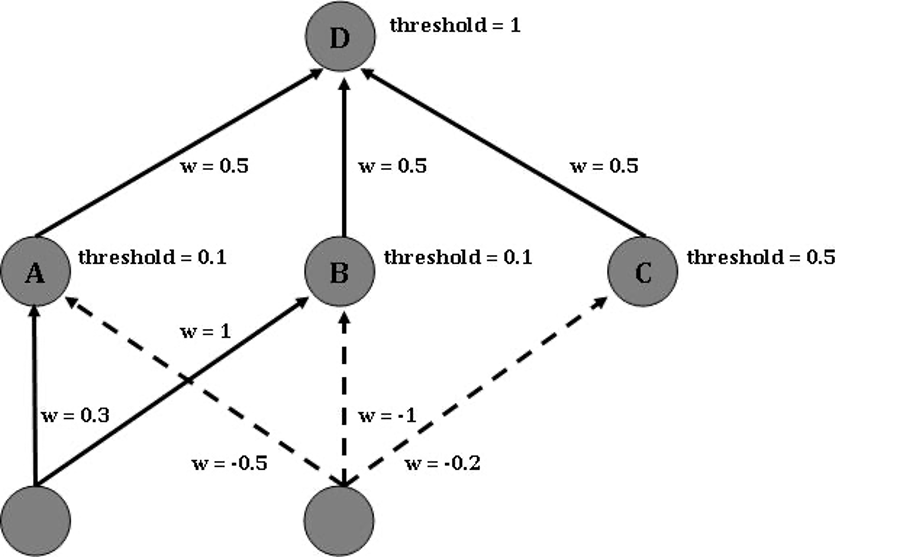
Activity 2.4: Three-Layer Neural Network
Create three truth tables for the network below: one for neuron A, one for neuron C, and one for D, which is the network as a whole. Note, the inputs for D are the outputs of A, B, & C, which themselves respond to the three input neurons. That is, you must calculate the truth tables for A, B, & C first, and use the output of those tables in your truth table for D. An example truth table for neuron D is shown below the network figure.

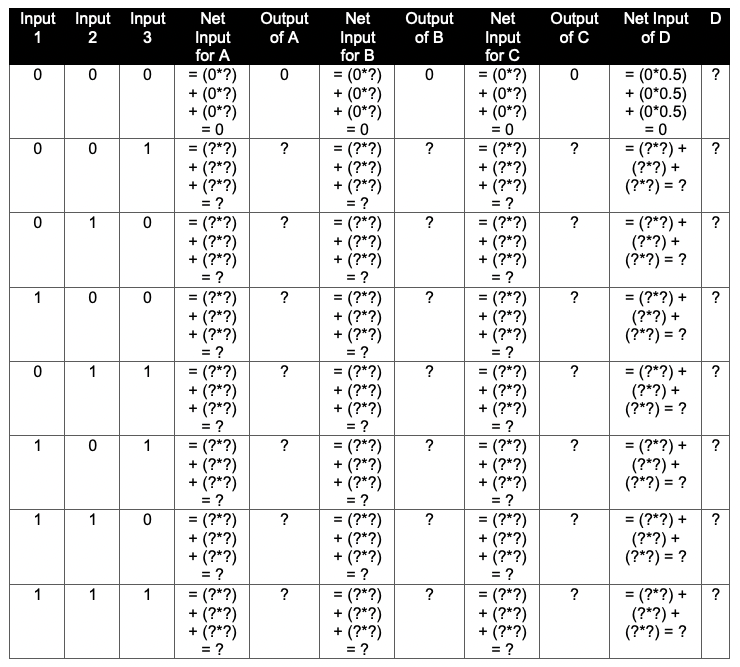 Now imagine that one of the inputs to this network was lesioned, as below. Create a new set of truth tables (A, B, C, D) reflecting the new relationship between Inputs and Output (D).
Now imagine that one of the inputs to this network was lesioned, as below. Create a new set of truth tables (A, B, C, D) reflecting the new relationship between Inputs and Output (D).
If you’d like to explore further with another fun “paper-and-pencil” neural network exercise, see this example of a demonstration of how a simple learning algorithm can cause a network to associate squirrel food (acorns) with spatial landmarks (trees).
- Neural systems can be examined from three distinct levels of analysis: implementational, algorithmic, and computational.
- Neurophysiology examines neurons from an implementational level of analysis.
- The integrate-and-fire model is one algorithmic representation of neurons from an information-processing perspective.
- At a more general functional level, neurons can be thought of as detectors.
- There are two prerequisites for a system to be able to process information:
- It must have components (e.g., transistors; neurons; dominos) which can switch between two states (e.g., electricity/no electricity; resting potential/action potential; standing/falling).
- The state of a component must be a function of connected components (such as activity from presynaptic neurons).
- Small networks of neurons can give rise to logical functions, like “inclusive-or”, “and”, and “exclusive-or”.
- Neural networks with four or more layers are “universal computers”, which can compute any computable function.
- Information processing can be abstracted away from the physical materials doing the processing. Even chains of dominos can work like computers (although extremely inefficiently).
Media Attributions
- Dynamic Neuron © Christopher J. May
- Inclusive Or © Christopher J. May
- Activity 2-1 to 2-2 © Christopher J. May is licensed under a CC0 (Creative Commons Zero) license
- And © Christopher J. May
- Neural Network E © Christopher J. May
- Neural Representations © Christopher J. May
- Exclusive Or © Christopher J. May
- Figure XOR © Christopher J. May is licensed under a CC0 (Creative Commons Zero) license
- Three Layer Network © Christopher J. May
- Activity 2-4 © Christopher J. May is licensed under a CC0 (Creative Commons Zero) license
- Three Layer Network Missing Input © Christopher May
- More accurately, neurons have a spontaneous firing rate when they are not being stimulated. In addition, the firing rates of neurons vary as a function of the similarity of a particular property to what it is tuned to detect (giving rise to “tuning curves”), and how intense a stimulus is (e.g., the loudness of a sound). ↵
- Neurons are often spontaneously active, however. The importance of spontaneous (rather than evoked) action potentials is an active area of investigation. ↵
- For an in-class demonstration, see May, C. (2010). Demonstrations of neural network computations involving students. Journal of Undergraduate Neuroscience Education, 8, 2, A116-A121. ↵
- More specifically, a three-layer network can compute any continuous function. ↵
