22 Setting up a Factorial Experiment

Experiments with Multiple Variables

Just as it is common for studies in business to include multiple levels of a single independent variable, it is also common for them to include multiple independent variables. The Werkman, Van Doorn & Van Ittersum (2021) study from a previous chapter also manipulated two variables: unit size (=cookie size) and serving size (amount of cookies).

Just as including multiple levels of a single independent variable allows one to answer more sophisticated research questions, so too does including multiple independent variables in the same experiment. Including multiple independent variables also allows the researcher to answer questions about whether the effect of one independent variable depends on the level of another. This is referred to as an ‘interaction’ between the independent variables, also called ‘moderation’.

Factorial Designs

Overview

By far the most common approach to including multiple independent variables (which are often called factors) in an experiment is the factorial design. In a factorial design, each level of one independent variable is combined with each level of the others to produce all possible combinations. Each combination, then, becomes a condition in the experiment. In the Werkman paper cited above, two variables (unit size and serving size) resulted in four conditions, being all possible combination of a large/small unit size and a large/small serving size. For another example, imagine an experiment on the effect of cell phone use (yes vs. no) and time of day (day vs. night) on driving ability. This is shown in the factorial design table in Figure 22.1. The columns of the table represent cell phone use, and the rows represent time of day. The four cells of the table represent the four possible combinations or conditions: using a cell phone during the day, not using a cell phone during the day, using a cell phone at night, and not using a cell phone at night. This particular design is referred to as a 2 × 2 (read “two-by-two”) factorial design because it combines two variables, each of which has two levels.

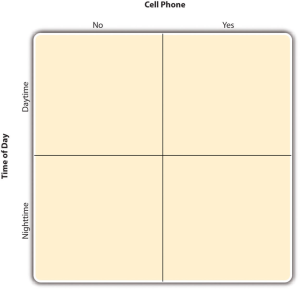
Figure 22.1 Factorial Design Table Representing a 2 × 2 Factorial Design

If one of the independent variables had a third level (e.g., using a handheld cell phone, using a hands-free cell phone, and not using a cell phone), then it would be a 3 × 2 factorial design, and there would be six distinct conditions. Notice that the number of possible conditions is the product of the numbers of levels. A 2 × 2 factorial design has four conditions, a 3 × 2 factorial design has six conditions, a 4 × 5 factorial design would have 20 conditions, and so on. Also notice that each number in the notation represents one factor, one independent variable. So by looking at how many numbers are in the notation, you can determine how many independent variables there are in the experiment. 2 x 2, 3 x 3, and 2 x 3 designs all have two numbers in the notation and therefore all have two independent variables. The numerical value of each of the numbers represents the number of levels of each independent variable. A 2 means that the independent variable has two levels, a 3 means that the independent variable has three levels, a 4 means it has four levels, etc. To illustrate a 3 x 3 design has two independent variables, each with three levels, while a 2 x 2 x 2 design has three independent variables, each with two levels.

In principle, factorial designs can include any number of independent variables with any number of levels. In practice, it is unusual for there to be more than three independent variables with more than two or three levels each. This is for at least two reasons: For one, the number of conditions can quickly become unmanageable. For example, adding a fourth independent variable with three levels to a 2 × 2 × 2 would make it a 2 × 2 × 2 × 3 factorial design with 24 distinct conditions. Second, the number of participants required to populate all of these conditions (while maintaining a reasonable ability to detect a real underlying effect) can render the design unfeasible. As a result, in the remainder of this section, we will focus on designs with two independent variables. The general principles discussed here extend in a straightforward way to more complex factorial designs.

Assigning Participants to Conditions

Recall that in a simple between-subjects design, each participant is tested in only one condition. In a simple within-subjects design, each participant is tested in all conditions. In a factorial experiment, the decision to take the between-subjects or within-subjects approach must be made separately for each independent variable. In most experiments in business research however, a between-subjects factorial design is used most often. In this design, all of the independent variables are manipulated between subjects.

Since factorial designs have more than one independent variable, it is also possible to manipulate one independent variable between subjects and another within subjects. This is called a mixed factorial design. For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone (while counterbalancing the order of these two conditions). But they might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). Thus each participant in this mixed design would be tested in two of the four conditions. Regardless of whether the design is between subjects, within subjects, or mixed, the actual assignment of participants to conditions or orders of conditions is typically done randomly.

Non-Manipulated Independent Variables

In many factorial designs, one of the independent variables is a non-manipulated independent variable. The researcher measures it but does not manipulate it. One example is a study by Halle Brown and colleagues in which participants were exposed to several words that they were later asked to recall (Brown, Kosslyn, Delamater, Fama, & Barsky, 1999)^[1]. The manipulated independent variable was the type of word. Some were negative health-related words (e.g., tumor, coronary), and others were not health related (e.g., election, geometry). The non-manipulated independent variable was whether participants were high or low in hypochondriasis (excessive concern with ordinary bodily symptoms). The result of this study was that the participants high in hypochondriasis were better than those low in hypochondriasis at recalling the health-related words, but they were no better at recalling the non-health-related words.

Such studies are extremely common, and there are several points worth making about them. First, non-manipulated independent variables are usually participant variables and as such, they are by definition between-subjects factors. For example, people are either low in hypochondriasis or high in hypochondriasis; they cannot be tested in both of these conditions. Second, such studies are generally considered to be experiments as long as at least one independent variable is manipulated, regardless of how many non-manipulated independent variables are included. Third, it is important to remember that causal conclusions can only be drawn about the manipulated independent variable.