4 Propositions, hypotheses, theories and models

Propositions and hypotheses

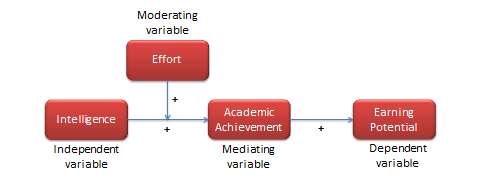
Figure 4.2 in the previous chapter (reprinted above) shows how theoretical constructs such as intelligence, effort, academic achievement, and earning potential are related to each other in a conceptual model. Each of these relationships is called a proposition. In seeking explanations for a given phenomenon or behaviour, it is not adequate just to identify key concepts and constructs underlying the target phenomenon or behaviour. We must also identify and state patterns of relationships between these constructs. Such patterns of relationships are called propositions. A proposition is a tentative and conjectural relationship between constructs that is stated in a declarative form. An example of a proposition is: ‘An increase in student intelligence causes an increase in their academic achievement’. This declarative statement does not have to be true, but must be empirically testable using data, so that we can judge whether it is true or false. Propositions are generally derived based on logic or empirical observations.

Because propositions are associations between abstract constructs, they cannot be tested directly. Instead, they are tested indirectly by examining the relationship between corresponding measures (variables) of those constructs. The empirical formulations of propositions, stated as relationships between variables, are called hypotheses (see Figure 4.1). Since IQ scores and GPAs are operational measures of intelligence and academic achievement respectively, the above proposition can be specified in form of the hypothesis: ‘An increase in students’ IQ score causes an increase in their GPA’. Propositions are specified in the theoretical plane, while hypotheses are specified in the empirical plane. Hence, hypotheses are empirically testable using observed data, and may be rejected if not supported by empirical observations. Of course, the goal of hypothesis testing is to infer whether the corresponding proposition is valid.

Hypotheses can be strong or weak. ‘Students’ IQ scores are related to their academic achievement’ is an example of a weak hypothesis, since it indicates neither the directionality of the hypothesis (i.e., whether the relationship is positive or negative), nor its causality (i.e., whether intelligence causes academic achievement or academic achievement causes intelligence). A stronger hypothesis is ‘students’ IQ scores are positively related to their academic achievement’, which indicates the directionality but not the causality. A still stronger hypothesis is ‘students’ IQ scores have positive effects on their academic achievement’, which specifies both the directionality and the causality (i.e., intelligence causes academic achievement, and not the reverse). The signs in Figure 4.2 indicate the directionality of the respective hypotheses.

One important thing to note about the signs in Figure 4.2 is the following: a ‘+’ sign signifies a positive relationship: if intelligence increases, academic achievement increases. Note that a positive sign also tells us something about what we expect to happen if intelligence decreases. If intelligence decreases, academic performance decreases. In other words, a positive sign indicates that two variables ‘move together’, in the same direction. A negative sign, in contrast, implies that variables move in the opposite direction. For example, more satisfied customers might switch less and less satisfied customers might switch more.

Also note that scientific hypotheses should clearly specify independent and dependent variables. In the hypothesis, ‘students’ IQ scores have positive effects on their academic achievement’, it is clear that intelligence is the independent variable (the ‘cause’) and academic achievement is the dependent variable (the ‘effect’). Further, it is also clear that this hypothesis can be evaluated as either true (if higher intelligence leads to higher academic achievement) or false (if higher intelligence has no effect on or leads to lower academic achievement). Statements such as ‘students are generally intelligent’ or ‘all students can achieve academic success’ are not scientific hypotheses because they do not specify independent and dependent variables, nor do they specify a directional relationship that can be evaluated as true or false.

Theories and models

Theories

A theory is a set of systematically interrelated constructs and propositions intended to explain and predict a phenomenon or behaviour of interest, within certain boundary conditions and assumptions. Essentially, a theory is a systemic collection of related theoretical propositions. While propositions generally connect two or three constructs, theories represent a system of multiple constructs and propositions. Hence, theories can be substantially more complex and abstract and of a larger scope than propositions or hypotheses.

I must note here that people unfamiliar with scientific research often view a theory as a speculation or the opposite of fact. For instance, people often say that teachers need to be less theoretical and more practical or factual in their classroom teaching. However, practice or fact are not opposites of theory, but in a scientific sense, are essential components needed to test the validity of a theory. A good scientific theory should be well supported using observed facts and should also have practical value, while a poorly defined theory tends to be lacking in these dimensions. Famous organisational researcher Kurt Lewin once said, ‘Theory without practice is sterile; practice without theory is blind’. Hence, both theory and facts (or practice) are essential for scientific research.

Theories provide explanations of social or natural phenomena. However, it is important for researchers to understand that theory is not ‘truth’, there is nothing sacrosanct about any theory, and theories should not be accepted just because they were proposed by someone. In the course of scientific progress, poorer theories are eventually replaced by better theories with higher explanatory power. The essential challenge for researchers is to build better and more comprehensive theories that can explain a target phenomenon better than prior theories.

Models

A term often used in conjunction with theory is a model. A model is a representation of all or part of a system that is constructed to study that system (e.g., how the system works or what triggers the system). While a theory tries to explain a phenomenon, a model tries to represent a phenomenon.

Models are often used by decision makers to make important decisions based on a given set of inputs. For instance, marketing managers may use models to decide how much money to spend on advertising for different product lines based on parameters such as prior year’s advertising expenses, sales, market growth, and competing products. Likewise, weather forecasters can use models to predict future weather patterns based on parameters such as wind speeds, wind direction, temperature, and humidity. While these models are useful, they may not necessarily explain advertising expenditure or weather forecasts.

Models may be of different kinds. In the context of this course and especially the statistics course, you will mainly encounter mathematical models. One example of this is regression analysis. Such models are tools which can be used for different purposes.

One purpose is to improve our understanding. A marketing researcher may run an experiment (see later chapter) to study the effect of advertising expenditure on the sales of their firm’s products. The may subsequently run a regression model which ‘models’ our hypothesis (that advertising causes sales) in a very specific mathematical way (as a linear equation, see later chapter). After doing so, the researcher obtains an estimate of how large the effect  of advertising on sales is. This may in turn inform decisions on how much to spend on advertising.

The same model can also be used for predicting: once we have a specific mathematical equation that relates advertising spending to sales, a manager is able to predict what their sales would be at a given level of advertising. Of course, this is a very simple example, and actual models in practice tend to be significantly more complicated.

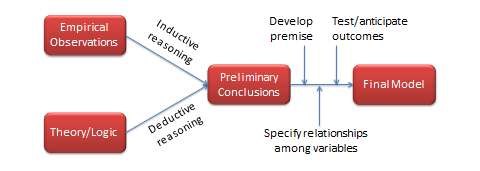
The process of theory building or model development may involve inductive and deductive reasoning. Deduction is the process of drawing conclusions about a phenomenon or behaviour based on theoretical or logical reasons and an initial set of premises. As an example, if a certain bank enforces a strict code of ethics for its employees (Premise 1), and Jamie is an employee at that bank (Premise 2), then Jamie can be trusted to follow ethical practices (Conclusion). In deduction, the conclusions must be true if the initial premises and reasons are correct.

In contrast, induction is the process of drawing conclusions based on facts or observed evidence. For instance, if a firm spent a lot of money on a promotional campaign (Observation 1), but the sales did not increase (Observation 2), then possibly the promotion campaign was poorly executed (Conclusion). However, there may be rival explanations for poor sales, such as economic recession or the emergence of a competing product or brand or perhaps a supply chain problem. Inductive conclusions are therefore only a hypothesis, and may be disproven. Deductive conclusions generally tend to be stronger than inductive conclusions, but a deductive conclusion based on an incorrect premise is also incorrect.

As shown in Figure 5.1, inductive and deductive reasoning go hand in hand in theory and model building. Induction occurs when we observe a fact and ask, ‘Why is this happening?’. In answering this question, we advance one or more tentative explanations (hypotheses). We then use deduction to narrow down the tentative explanations to the most plausible explanation based on logic and reasonable premises (based on our understanding of the phenomenon under study). Researchers must be able to move back and forth between inductive and deductive reasoning if they are to post extensions or modifications to a given model or theory, or build better ones, both of which are the essence of scientific research.